Reference¶

Accessor Methods¶

The following methods are available via traja.accessor.TrajaAccessor:

class traja.accessor.TrajaAccessor(pandas_obj)[source]

Accessor for pandas DataFrame with trajectory-specific numerical and analytical functions.

Access with df.traja.

property center: Return the center point of this trajectory.

property bounds: Return limits of x and y dimensions ((xmin, xmax), (ymin, ymax)).

night(begin: str = '19:00', end: str = '7:00')[source]

Get nighttime dataset between begin and end.

Parameters

begin (str) – (Default value = ‘19:00’)
end (str) – (Default value = ‘7:00’)

Returns

Trajectory during night.

Return type

trj (TrajaDataFrame)

day(begin: str = '7:00', end: str = '19:00')[source]

Get daytime dataset between begin and end.

Parameters

begin (str) – (Default value = ‘7:00’)
end (str) – (Default value = ‘19:00’)

Returns

Trajectory during day.

Return type

trj (TrajaDataFrame)

_get_time_col()[source]

Returns time column in trajectory.

Args:

Returns: name of time column, ‘index’ or None
Return type: time_col (str or None)

between(begin: str, end: str)[source]

Returns trajectory between begin and end` if time column is datetime64.

Parameters

begin (str) – Beginning of time slice.
end (str) – End of time slice.

Returns

Dataframe between values.

Return type

trj (TrajaDataFrame)

>>> s = pd.to_datetime(pd.Series(['Jun 30 2000 12:00:01', 'Jun 30 2000 12:00:02', 'Jun 30 2000 12:00:03']))
>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3],'time':s})
>>> df.traja.between('12:00:00','12:00:01')
                 time  x  y
0 2000-06-30 12:00:01  0  1

resample_time(step_time: float)[source]

Returns trajectory resampled with step_time.

Parameters: step_time (float) – Step time
Returns: Dataframe resampled.
Return type: trj (TrajaDataFrame)

rediscretize_points(R, **kwargs)[source]: Rediscretize points

trip_grid(bins: Union[int, tuple] = 10, log: bool = False, spatial_units=None, normalize: bool = False, hist_only: bool = False, plot: bool = True, **kwargs)[source]

Returns a 2D histogram of trip.

Parameters

bins (int, optional) – Number of bins (Default value = 16)
log (bool) – log scale histogram (Default value = False)
spatial_units (str) – units for plotting
normalize (bool) – normalize histogram into density plot
hist_only (bool) – return histogram without plotting

Returns

2D histogram as array image (matplotlib.collections.PathCollection: image of histogram

Return type

hist (numpy.ndarray)

plot(n_coords: Optional[int] = None, show_time=False, **kwargs)[source]

Plot trajectory over period.

Parameters

n_coords (int) – Number of coordinates to plot
**kwargs – additional keyword arguments to matplotlib.axes.Axes.scatter()

Returns

Axes of plot

Return type

ax (Axes)

plot_3d(**kwargs)[source]

Plot 3D trajectory for single identity over period.

Args: trj (traja.TrajaDataFrame): trajectory n_coords (int, optional): Number of coordinates to plot **kwargs: additional keyword arguments to matplotlib.axes.Axes.scatter()

Returns: collection that was plotted
Return type: collection (PathCollection)

Note

Takes a while to plot large trajectories. Consider using first:

rt = trj.traja.rediscretize(R=1.) # Replace R with appropriate step length
rt.traja.plot_3d()

plot_flow(kind='quiver', **kwargs)[source]

Plot grid cell flow.

Parameters

kind (str) – Kind of plot (eg, ‘quiver’,’surface’,’contour’,’contourf’,’stream’)
**kwargs – additional keyword arguments to matplotlib.axes.Axes.scatter()

Returns

Axes of plot

Return type

ax (Axes)

plot_collection(colors=None, **kwargs)[source]

apply_all(method, id_col=None, **kwargs)[source]: Applies method to all trajectories and returns grouped dataframes or series

property xy

Returns a numpy.ndarray of x,y coordinates.

Parameters: split (bool) – Split into seaprate x and y numpy.ndarrays
Returns: xy (numpy.ndarray) – x,y coordinates (separate if split is True)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> df.traja.xy
array([[0, 1],
       [1, 2],
       [2, 3]])

_check_has_time()[source]: Check for presence of displacement time column.

__getattr__(name)[source]: Catch all method calls which are not defined and forward to modules.

transitions(*args, **kwargs)[source]: Calculate transition matrix

calc_derivatives(assign: bool = False)[source]

Returns derivatives displacement and displacement_time.

Parameters: assign (bool) – Assign output to TrajaDataFrame (Default value = False)
Returns: Derivatives.
Return type: derivs (OrderedDict)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3],'time':[0., 0.2, 0.4]})
>>> df.traja.calc_derivatives()
   displacement  displacement_time
0           NaN                0.0
1      1.414214                0.2
2      1.414214                0.4

get_derivatives() → DataFrame[source]: Returns derivatives as DataFrame.

speed_intervals(faster_than: Optional[Union[float, int]] = None, slower_than: Optional[Union[float, int]] = None)[source]

Returns TrajaDataFrame with speed time intervals.

Returns a dataframe of time intervals where speed is slower and/or faster than specified values.

Parameters

faster_than (float, optional) – Minimum speed threshold. (Default value = None)
slower_than (float or int, optional) – Maximum speed threshold. (Default value = None)

Returns

result (DataFrame) – time intervals as dataframe

Note

Implementation ported to Python, heavily inspired by Jim McLean’s trajr package.

to_shapely()[source]

Returns shapely object for area, bounds, etc. functions.

Args:

Returns: Shapely shape.
Return type: shape (shapely.geometry.linestring.LineString)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> shape = df.traja.to_shapely()
>>> shape.is_closed
False

calc_displacement(assign: bool = True) → Series[source]

Returns Series of float with displacement between consecutive indices.

Parameters: assign (bool, optional) – Assign displacement to TrajaAccessor (Default value = True)
Returns: Displacement series.
Return type: displacement (pandas.Series)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> df.traja.calc_displacement()
0         NaN
1    1.414214
2    1.414214
Name: displacement, dtype: float64

calc_angle(assign: bool = True) → Series[source]

Returns Series with angle between steps as a function of displacement with regard to x axis.

Parameters: assign (bool, optional) – Assign turn angle to TrajaAccessor (Default value = True)
Returns: Angle series.
Return type: angle (pandas.Series)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> df.traja.calc_angle()
0     NaN
1    45.0
2    45.0
dtype: float64

scale(scale: float, spatial_units: str = 'm')[source]

Scale trajectory when converting, eg, from pixels to meters.

Parameters

scale (float) – Scale to convert coordinates
spatial_units (str., optional) – Spatial units (eg, ‘m’) (Default value = “m”)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> df.traja.scale(0.1)
>>> df
     x    y
0  0.0  0.1
1  0.1  0.2
2  0.2  0.3

rediscretize(R: float)[source]

Resample a trajectory to a constant step length. R is rediscretized step length.

Parameters: R (float) – Rediscretized step length (eg, 0.02)
Returns: rediscretized trajectory
Return type: rt (traja.TrajaDataFrame)

Note

Based on the appendix in Bovet and Benhamou, (1988) and Jim McLean’s trajr implementation.

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> df.traja.rediscretize(1.)
          x         y
0  0.000000  1.000000
1  0.707107  1.707107
2  1.414214  2.414214

grid_coordinates(**kwargs)[source]

calc_heading(assign: bool = True)[source]

Calculate trajectory heading.

Parameters: assign (bool) – (Default value = True)
Returns: heading as a Series
Return type: heading (pandas.Series)

..doctest:

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> df.traja.calc_heading()
0     NaN
1    45.0
2    45.0
Name: heading, dtype: float64

calc_turn_angle(assign: bool = True)[source]

Calculate turn angle.

Parameters: assign (bool) – (Default value = True)
Returns: Turn angle
Return type: turn_angle (Series)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> df.traja.calc_turn_angle()
0    NaN
1    NaN
2    0.0
Name: turn_angle, dtype: float64

Plotting functions¶

The following methods are available via traja.plotting:

plotting.animate(polar: bool = True, save: bool = False)¶

Animate trajectory.

Parameters

polar (bool) – include polar bar chart with turn angle
save (bool) – save video to trajectory.mp4

Returns

animation

Return type

anim (matplotlib.animation.FuncAnimation)

plotting.bar_plot(bins: Optional[Union[int, tuple]] = None, **kwargs) → Axes¶

Plot trajectory for single animal over period.

Parameters

trj (traja.TrajaDataFrame) – trajectory
bins (int or tuple) – number of bins for x and y
**kwargs – additional keyword arguments to mpl_toolkits.mplot3d.Axed3D.plot()

Returns

Axes of plot

Return type

ax (PathCollection)

plotting.color_dark(ax: Optional[Axes] = None, start: int = 19, end: int = 7)¶

Color dark phase in plot. :param series: :type series: pd.Series :param ax (: class: ~matplotlib.axes.Axes): axis to plot on (eg, plt.gca()) :param start: start of dark period/night :type start: int :param end: end of dark period/day :type end: hour

Returns: Axes of plot
Return type: ax (AxesSubplot)

plotting.fill_ci(window: Union[int, str]) → Figure¶: Fill confidence interval defined by SEM over mean of window. Window can be interval or offset, eg, ’30s’.

plotting.find_runs() -> (<class 'numpy.ndarray'>, <class 'numpy.ndarray'>, <class 'numpy.ndarray'>)¶: Find runs of consecutive items in an array. From https://gist.github.com/alimanfoo/c5977e87111abe8127453b21204c1065.

plotting.plot(n_coords: Optional[int] = None, show_time: bool = False, accessor: Optional[TrajaAccessor] = None, ax=None, **kwargs) → PathCollection¶

Plot trajectory for single animal over period.

Parameters

trj (traja.TrajaDataFrame) – trajectory
n_coords (int, optional) – Number of coordinates to plot
show_time (bool) – Show colormap as time
accessor (TrajaAccessor, optional) – TrajaAccessor instance
ax (Axes) – axes for plotting
interactive (bool) – show plot immediately
**kwargs – additional keyword arguments to matplotlib.axes.Axes.scatter()

Returns

collection that was plotted

Return type

collection (PathCollection)

plotting.plot_3d(**kwargs) → PathCollection¶

Plot 3D trajectory for single identity over period.

Parameters

trj (traja.TrajaDataFrame) – trajectory
n_coords (int, optional) – Number of coordinates to plot
**kwargs – additional keyword arguments to matplotlib.axes.Axes.scatter()

Returns

Axes of plot

Return type

ax (PathCollection)

Note

Takes a while to plot large trajectories. Consider using first:

rt = trj.traja.rediscretize(R=1.) # Replace R with appropriate step length
rt.traja.plot_3d()

plotting.plot_actogram(dark=(19, 7), ax: Optional[Axes] = None, **kwargs)¶: Plot activity or displacement as an actogram.

Note

For published example see Eckel-Mahan K, Sassone-Corsi P. Phenotyping Circadian Rhythms in Mice. Curr Protoc Mouse Biol. 2015;5(3):271-281. Published 2015 Sep 1. doi:10.1002/9780470942390.mo140229

plotting.plot_autocorrelation(coord: str = 'y', unit: str = 'Days', xmax: int = 1000, interactive: bool = True)¶

Plot autocorrelation of given coordinate.

Parameters

Trajectory (trj -) –
'y' (coord - 'x' or) –
string (unit -) –
eg –
'Days' –
value (xmax - max xaxis) –
immediately (interactive - Plot) –

Returns

Matplotlib Figure

(Source code, png, hires.png, pdf)

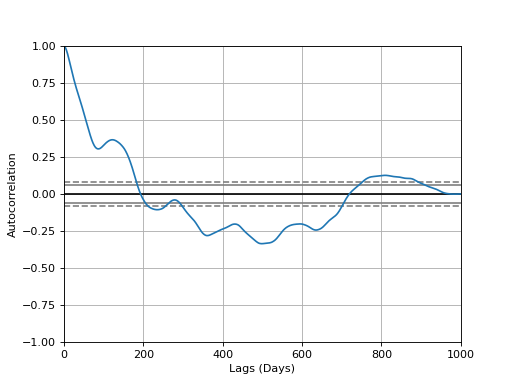
Note

Convenience wrapper for pandas autocorrelation_plot().

plotting.plot_contour(bins: Optional[Union[int, tuple]] = None, filled: bool = True, quiver: bool = True, contourplot_kws: dict = {}, contourfplot_kws: dict = {}, quiverplot_kws: dict = {}, ax: Optional[Axes] = None, **kwargs) → Axes¶

Plot average flow from each grid cell to neighbor.

Parameters

trj – Traja DataFrame
bins (int or tuple) – Tuple of x,y bin counts; if bins is int, bin count of x, with y inferred from aspect ratio
filled (bool) – Contours filled
quiver (bool) – Quiver plot
contourplot_kws – Additional keyword arguments for contour()
contourfplot_kws – Additional keyword arguments for contourf()
quiverplot_kws – Additional keyword arguments for quiver()
ax (optional) – Matplotlib Axes

Returns

Axes of quiver plot

Return type

ax (Axes)

plotting.plot_clustermap(rule: Optional[str] = None, nr_steps=None, colors: Optional[List[Union[int, str]]] = None, **kwargs)¶

Plot cluster map / dendrogram of trajectories with DatetimeIndex.

Parameters

displacements – list of pd.Series, outputs of traja.calc_displacement()
rule – how to resample series, eg ’30s’ for 30-seconds
nr_steps – select first N samples for clustering
colors – list of colors (eg, ‘b’,’r’) to map to each trajectory
kwargs – keyword arguments for seaborn.clustermap()

Returns

a seaborn.matrix.ClusterGrid() instance

Return type

cg

Note

Requires seaborn to be installed. Install it with ‘pip install seaborn’.

plotting.plot_flow(kind: str = 'quiver', *args, contourplot_kws: dict = {}, contourfplot_kws: dict = {}, streamplot_kws: dict = {}, quiverplot_kws: dict = {}, surfaceplot_kws: dict = {}, **kwargs) → Figure¶

Plot average flow from each grid cell to neighbor.

Parameters

bins (int or tuple) – Tuple of x,y bin counts; if bins is int, bin count of x, with y inferred from aspect ratio
kind (str) – Choice of ‘quiver’,’contourf’,’stream’,’surface’. Default is ‘quiver’.
contourplot_kws – Additional keyword arguments for contour()
contourfplot_kws – Additional keyword arguments for contourf()
streamplot_kws – Additional keyword arguments for streamplot()
quiverplot_kws – Additional keyword arguments for quiver()
surfaceplot_kws – Additional keyword arguments for plot_surface()

Returns

Axes of plot

Return type

ax (Axes)

plotting.plot_quiver(bins: Optional[Union[int, tuple]] = None, quiverplot_kws: dict = {}, **kwargs) → Axes¶

Plot average flow from each grid cell to neighbor.

Parameters

bins (int or tuple) – Tuple of x,y bin counts; if bins is int, bin count of x, with y inferred from aspect ratio
quiverplot_kws – Additional keyword arguments for quiver()

Returns

Axes of quiver plot

Return type

ax (Axes)

plotting.plot_stream(bins: Optional[Union[int, tuple]] = None, cmap: str = 'viridis', contourfplot_kws: dict = {}, contourplot_kws: dict = {}, streamplot_kws: dict = {}, **kwargs) → Figure¶

Plot average flow from each grid cell to neighbor.

Parameters

bins (int or tuple) – Tuple of x,y bin counts; if bins is int, bin count of x, with y inferred from aspect ratio
contourplot_kws – Additional keyword arguments for contour()
contourfplot_kws – Additional keyword arguments for contourf()
streamplot_kws – Additional keyword arguments for streamplot()

Returns

Axes of stream plot

Return type

ax (Axes)

plotting.plot_surface(bins: Optional[Union[int, tuple]] = None, cmap: str = 'viridis', **surfaceplot_kws: dict) → Figure¶

Plot surface of flow from each grid cell to neighbor in 3D.

Parameters

bins (int or tuple) – Tuple of x,y bin counts; if bins is int, bin count of x, with y inferred from aspect ratio
cmap (str) – color map
surfaceplot_kws – Additional keyword arguments for plot_surface()

Returns

Axes of quiver plot

Return type

ax (Axes)

plotting.plot_transition_matrix(interactive=True, **kwargs) → AxesImage¶

Plot transition matrix.

Parameters

data (trajectory or square transition matrix) –
interactive (bool) – show plot
kwargs – kwargs to traja.grid_coordinates()

Returns

axesimage (matplotlib.image.AxesImage)

plotting.plot_xy(*args: Optional, **kwargs: Optional)¶

Plot trajectory from xy values.

Parameters

xy (np.ndarray) – xy values of dimensions N x 2
*args – Plot args
**kwargs – Plot kwargs

plotting.polar_bar(feature: str = 'turn_angle', bin_size: int = 2, threshold: float = 0.001, overlap: bool = True, ax: Optional[Axes] = None, **plot_kws: str) → Axes¶

Plot polar bar chart.

Parameters

trj (traja.TrajaDataFrame) – trajectory
feature (str) – Options: ‘turn_angle’, ‘heading’
bin_size (int) – width of bins
threshold (float) – filter for step distance
overlap (bool) – Overlapping shows all values, if set to false is a histogram

Returns

Axes of plot

Return type

ax (PathCollection)

plotting.plot_prediction(dataloader, index, scaler=None)¶

plotting.sans_serif()¶: Convenience function for changing plot text to serif font.

plotting.stylize_axes()¶: Add top and right border to plot, set ticks.

plotting.trip_grid(bins: Union[tuple, int] = 10, log: bool = False, spatial_units: Optional[str] = None, normalize: bool = False, hist_only: bool = False, **kwargs) → Tuple[ndarray, PathCollection]¶

Generate a heatmap of time spent by point-to-cell gridding.

Parameters

bins (int, optional) – Number of bins (Default value = 10)
log (bool) – log scale histogram (Default value = False)
spatial_units (str) – units for plotting
normalize (bool) – normalize histogram into density plot
hist_only (bool) – return histogram without plotting

Returns

2D histogram as array image (matplotlib.collections.PathCollection: image of histogram

Return type

hist (numpy.ndarray)

Analysis¶

The following methods are available via traja.trajectory:

trajectory.calc_angle(unit: str = 'degrees', lag: int = 1)¶

Returns a Series with angle between steps as a function of displacement with regard to x axis.

Parameters

trj (TrajaDataFrame) – Trajectory
unit (str) – return angle in radians or degrees (Default value: ‘degrees’)
lag (int) – time steps between angle calculation (Default value: 1)

Returns

Angle series.

Return type

angle (pandas.Series)

trajectory.calc_convex_hull() → array¶

Identify containing polygonal convex hull for full Trajectory Interior points filtered with traja.trajectory.inside() method, takes quadrilateral using extrema points (minx, maxx, miny, maxy) - convex hull points MUST all be outside such a polygon. Returns an array with all points in the convex hull.

Implementation of Graham Scan technique <https://en.wikipedia.org/wiki/Graham_scan>_.

Returns: n x 2 (x,y) array
Return type: point_arr (ndarray)

>> #Quick visualizaation
>> import matplotlib.pyplot as plt
>> df = traja.generate(n=10000, convex_hull=True)
>> xs, ys = [*zip(*df.convex_hull)]
>> _ = plt.plot(df.x.values, df.y.values, 'o', 'blue')
>> _ = plt.plot(xs, ys, '-o', color='red')
>> _ = plt.show()

Note

Incorporates Akl-Toussaint method for filtering interior points.

Note

Performative loss beyond ~100,000-200,000 points, algorithm has O(nlogn) complexity.

trajectory.calc_derivatives()¶

Returns derivatives displacement and displacement_time as DataFrame.

Parameters: trj (TrajaDataFrame) – Trajectory
Returns: Derivatives.
Return type: derivs (DataFrame)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3],'time':[0., 0.2, 0.4]})
>>> traja.calc_derivatives(df)
   displacement  displacement_time
0           NaN                0.0
1      1.414214                0.2
2      1.414214                0.4

trajectory.calc_displacement(lag=1)¶

Returns a Series of float displacement between consecutive indices.

Parameters

trj (TrajaDataFrame) – Trajectory
lag (int) – time steps between displacement calculation

Returns

Displacement series.

Return type

displacement (pandas.Series)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> traja.calc_displacement(df)
0         NaN
1    1.414214
2    1.414214
Name: displacement, dtype: float64

trajectory.calc_heading()¶

Calculate trajectory heading.

Parameters: trj (TrajaDataFrame) – Trajectory
Returns: heading as a Series
Return type: heading (pandas.Series)

..doctest:

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> traja.calc_heading(df)
0     NaN
1    45.0
2    45.0
Name: heading, dtype: float64

trajectory.calc_turn_angle()¶

Return a Series of floats with turn angles.

Parameters: trj (traja.frame.TrajaDataFrame) – Trajectory
Returns: Turn angle
Return type: turn_angle (Series)

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> traja.calc_turn_angle(df)
0    NaN
1    NaN
2    0.0
Name: turn_angle, dtype: float64

trajectory.calc_flow_angles()¶: Calculate average flow between grid indices.

trajectory.cartesian_to_polar() -> (<class 'float'>, <class 'float'>)¶

Convert numpy.ndarray xy to polar coordinates r and theta.

Parameters: xy (numpy.ndarray) – x,y coordinates
Returns: step-length and angle
Return type: r, theta (tuple of float)

trajectory.coords_to_flow(bins: Optional[Union[int, tuple]] = None)¶

Calculate grid cell flow from trajectory.

Parameters

trj (trajectory) –
bins (int or tuple) –

Returns

X coordinates of arrow locations Y (ndarray): Y coordinates of arrow locations U (ndarray): X component of vector dataset V (ndarray): Y component of vector dataset

Return type

X (ndarray)

trajectory.determine_colinearity(p1: ndarray, p2: ndarray)¶

Determine whether trio of points constitute a right turn, or whether they are left turns (or colinear/straight line).

Parameters

p0 (ndarray) – First point [x,y] in line
p1 (ndarray) – Second point [x,y] in line
p2 (ndarray) – Third point [x,y] in line

Returns

(bool)

trajectory.distance_between(B: TrajaDataFrame, method='dtw')¶

Returns distance between two trajectories.

Parameters

A (TrajaDataFrame) – Trajectory 1
B (TrajaDataFrame) – Trajectory 2
method (str) – dtw for dynamic time warping, hausdorff for Hausdorff

Returns

Distance

Return type

distance (float)

trajectory.distance() → float¶

Calculates the distance from start to end of trajectory, also called net distance, displacement, or bee-line from start to finish.

Parameters: trj (TrajaDataFrame) – Trajectory
Returns: distance (float)

>> df = traja.generate()
>> traja.distance(df)
117.01507823153617

trajectory.euclidean(v, w=None)¶

Computes the Euclidean distance between two 1-D arrays.

The Euclidean distance between 1-D arrays u and v, is defined as

\[ \begin{align}\begin{aligned}{||u-v||}_2\\\left(\sum{(w_i |(u_i - v_i)|^2)}\right)^{1/2}\end{aligned}\end{align} \]

Parameters

u ((N,) array_like) – Input array.
v ((N,) array_like) – Input array.
w ((N,) array_like, optional) – The weights for each value in u and v. Default is None, which gives each value a weight of 1.0

Returns

euclidean – The Euclidean distance between vectors u and v.

Return type

double

Examples

>>> from scipy.spatial import distance
>>> distance.euclidean([1, 0, 0], [0, 1, 0])
1.4142135623730951
>>> distance.euclidean([1, 1, 0], [0, 1, 0])
1.0

trajectory.expected_sq_displacement(n: int = 0, eqn1: bool = True) → float¶: Expected displacement.

Note

This method is experimental and needs testing.

trajectory.fill_in_traj()¶

trajectory.from_xy()¶

Convenience function for initializing TrajaDataFrame with x,y coordinates.

Parameters: xy (numpy.ndarray) – x,y coordinates
Returns: Trajectory as dataframe
Return type: traj_df (TrajaDataFrame)

>>> import numpy as np
>>> xy = np.array([[0,1],[1,2],[2,3]])
>>> traja.from_xy(xy)
   x  y
0  0  1
1  1  2
2  2  3

trajectory.generate(random: bool = True, step_length: int = 2, angular_error_sd: float = 0.5, angular_error_dist: Optional[Callable] = None, linear_error_sd: float = 0.2, linear_error_dist: Optional[Callable] = None, fps: float = 50, spatial_units: str = 'm', seed: Optional[int] = None, convex_hull: bool = False, **kwargs)¶

Generates a trajectory.

If random is True, the trajectory will be a correlated random walk/idiothetic directed walk (Kareiva & Shigesada, 1983), corresponding to an animal navigating without a compass (Cheung, Zhang, Stricker, & Srinivasan, 2008). If random is False, it will be(np.ndarray) a directed walk/allothetic directed walk/oriented path, corresponding to an animal navigating with a compass (Cheung, Zhang, Stricker, & Srinivasan, 2007, 2008).

By default, for both random and directed walks, errors are normally distributed, unbiased, and independent of each other, so are simple directed walks in the terminology of Cheung, Zhang, Stricker, & Srinivasan, (2008). This behaviour may be modified by specifying alternative values for the angular_error_dist and/or linear_error_dist parameters.

The initial angle (for a random walk) or the intended direction (for a directed walk) is 0 radians. The starting position is (0, 0).

Parameters

n (int) – (Default value = 1000)
random (bool) – (Default value = True)
step_length – (Default value = 2)
angular_error_sd (float) – (Default value = 0.5)
angular_error_dist (Callable) – (Default value = None)
linear_error_sd (float) – (Default value = 0.2)
linear_error_dist (Callable) – (Default value = None)
fps (float) – (Default value = 50)
convex_hull (bool) – (Default value = False)
spatial_units – (Default value = ‘m’)
**kwargs – Additional arguments

Returns

Trajectory

Return type

trj (traja.frame.TrajaDataFrame)

Note

Based on Jim McLean’s trajr, ported to Python.

Reference: McLean, D. J., & Skowron Volponi, M. A. (2018). trajr: An R package for characterisation of animal trajectories. Ethology, 124(6), 440-448. https://doi.org/10.1111/eth.12739.

trajectory.get_derivatives()¶

Returns derivatives displacement, displacement_time, speed, speed_times, acceleration, acceleration_times as dictionary.

Parameters: trj (TrajaDataFrame) – Trajectory
Returns: Derivatives
Return type: derivs (DataFrame)

>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3],'time':[0.,0.2,0.4]})
>> df.traja.get_derivatives() 
   displacement  displacement_time     speed  speed_times  acceleration  acceleration_times
0           NaN                0.0       NaN          NaN           NaN                 NaN
1      1.414214                0.2  7.071068          0.2           NaN                 NaN
2      1.414214                0.4  7.071068          0.4           0.0                 0.4

trajectory.grid_coordinates(bins: Optional[Union[int, tuple]] = None, xlim: Optional[tuple] = None, ylim: Optional[tuple] = None, assign: bool = False)¶

Returns DataFrame of trajectory discretized into 2D lattice grid coordinates. :param trj: Trajectory :type trj: ~`traja.frame.TrajaDataFrame` :param bins: :type bins: tuple or int :param xlim: :type xlim: tuple :param ylim: :type ylim: tuple :param assign: Return updated original dataframe :type assign: bool

Returns: Trajectory is assign=True otherwise pd.DataFrame
Return type: trj (TrajaDataFrame`)

trajectory.inside(bounds_xs: list, bounds_ys: list, minx: float, maxx: float, miny: float, maxy: float)¶

Determine whether point lies inside or outside of polygon formed by “extrema” points - minx, maxx, miny, maxy. Optimized to be run as broadcast function in numpy along axis.

Parameters

pt (ndarray) – Point to test whether inside or outside polygon
bounds_xs (list or tuple) – x-coordinates of polygon vertices, in sequence
bounds_ys (list or tuple) – y-coordinates of polygon vertices, same sequence
minx (float) – minimum x coordinate value
maxx (float) – maximum x coordinate value
miny (float) – minimum y coordinate value
maxy (float) – maximum y coordinate value

Returns

(bool)

Note

Ported to Python from C implementation by W. Randolph Franklin (WRF): <https://wrf.ecse.rpi.edu/Research/Short_Notes/pnpoly.html>

Boolean return “True” for OUTSIDE polygon, meaning it is within subset of possible convex hull coordinates.

trajectory.length() → float¶

Calculates the cumulative length of a trajectory.

Parameters: trj (TrajaDataFrame) – Trajectory
Returns: length (float)

>> df = traja.generate()
>> traja.length(df)
2001.142339606066

trajectory.polar_to_z(theta: float) → complex¶

Converts polar coordinates r and theta to complex number z.

Parameters

r (float) – step size
theta (float) – angle

Returns

complex number z

Return type

z (complex)

trajectory.rediscretize_points(R: Union[float, int], time_out=False)¶

Returns a TrajaDataFrame rediscretized to a constant step length R.

Parameters

trj (traja.frame.TrajaDataFrame) – Trajectory
R (float) – Rediscretized step length (eg, 0.02)
time_out (bool) – Include time corresponding to time intervals in output

Returns

rediscretized trajectory

Return type

rt (numpy.ndarray)

trajectory.resample_time(step_time: str, new_fps: Optional[bool] = None)¶

Returns a TrajaDataFrame resampled to consistent step_time intervals.

step_time should be expressed as a number-time unit combination, eg “2S” for 2 seconds and “2100L” for 2100 milliseconds.

Parameters

trj (TrajaDataFrame) – Trajectory
step_time (str) – step time interval / offset string (eg, ‘2S’ (seconds), ‘50L’ (milliseconds), ‘50N’ (nanoseconds))
new_fps (bool, optional) – new fps

Results:: trj (TrajaDataFrame): Trajectory

>>> from traja import generate, resample_time
>>> df = generate()
>>> resampled = resample_time(df, '50L') # 50 milliseconds
>>> resampled.head() 
                                 x         y
time
1970-01-01 00:00:00.000   0.000000  0.000000
1970-01-01 00:00:00.050   0.919113  4.022971
1970-01-01 00:00:00.100  -1.298510  5.423373
1970-01-01 00:00:00.150  -6.057524  4.708803
1970-01-01 00:00:00.200 -10.347759  2.108385

trajectory.return_angle_to_point(p0: ndarray)¶

Calculate angle of points as coordinates in relation to each other. Designed to be broadcast across all trajectory points for a single origin point p0.

Parameters

p1 (np.ndarray) – Test point [x,y]
p0 (np.ndarray) – Origin/source point [x,y]

Returns

r (float)

trajectory.rotate(angle: Union[float, int] = 0, origin: Optional[tuple] = None)¶

Returns a TrajaDataFrame Rotate a trajectory angle in radians.

Parameters

trj (traja.frame.TrajaDataFrame) – Trajectory
angle (float) – angle in radians
origin (tuple. optional) – rotate around point (x,y)

Returns

Trajectory

Return type

trj (traja.frame.TrajaDataFrame)

Note

Based on Lyle Scott’s implementation.

trajectory.smooth_sg(w: Optional[int] = None, p: int = 3)¶

Returns DataFrame of trajectory after Savitzky-Golay filtering.

Parameters

trj (TrajaDataFrame) – Trajectory
w (int) – window size (Default value = None)
p (int) – polynomial order (Default value = 3)

Returns

Trajectory

Return type

trj (TrajaDataFrame)

>> df = traja.generate()
>> traja.smooth_sg(df, w=101).head()
           x          y  time
0 -11.194803  12.312742  0.00
1 -10.236337  10.613720  0.02
2  -9.309282   8.954952  0.04
3  -8.412910   7.335925  0.06
4  -7.546492   5.756128  0.08

trajectory.speed_intervals(faster_than: Optional[float] = None, slower_than: Optional[float] = None) → DataFrame¶

Calculate speed time intervals.

Returns a dictionary of time intervals where speed is slower and/or faster than specified values.

Parameters

faster_than (float, optional) – Minimum speed threshold. (Default value = None)
slower_than (float or int, optional) – Maximum speed threshold. (Default value = None)

Returns

result (DataFrame) – time intervals as dataframe

Note

Implementation ported to Python, heavily inspired by Jim McLean’s trajr package.

>> df = traja.generate()
>> intervals = traja.speed_intervals(df, faster_than=100)
>> intervals.head()
   start_frame  start_time  stop_frame  stop_time  duration
0            1        0.02           3       0.06      0.04
1            4        0.08           8       0.16      0.08
2           10        0.20          11       0.22      0.02
3           12        0.24          15       0.30      0.06
4           17        0.34          18       0.36      0.02

trajectory.step_lengths()¶

Length of the steps of trj.

Parameters: trj (TrajaDataFrame) – Trajectory

trajectory.to_shapely()¶

Returns shapely object for area, bounds, etc. functions.

Parameters: trj (TrajaDataFrame) – Trajectory
Returns: shapely.geometry.linestring.LineString – Shapely shape.

>>> df = traja.TrajaDataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> shape = traja.to_shapely(df)
>>> shape.is_closed
False

trajectory.traj_from_coords(x_col=1, y_col=2, time_col: Optional[str] = None, fps: Union[float, int] = 4, spatial_units: str = 'm', time_units: str = 's') → TrajaDataFrame¶

Create TrajaDataFrame from coordinates.

Parameters

track – N x 2 numpy array or pandas DataFrame with x and y columns
x_col – column index or x column name
y_col – column index or y column name
time_col – name of time column
fps – Frames per seconds
spatial_units – default m, optional
time_units – default s, optional

Returns

TrajaDataFrame

Return type

trj

>> xy = np.random.random((1000, 2))
>> trj = traja.traj_from_coord(xy)
>> assert trj.shape == (1000,4) # columns x, y, time, dt

trajectory.transition_matrix()¶

Returns np.ndarray of Markov transition probability matrix for grid cell transitions.

Parameters: grid_indices1D (np.ndarray) –
Returns: M (numpy.ndarray)

trajectory.transitions(**kwargs)¶

Get first-order Markov model for transitions between grid cells.

Parameters

trj (trajectory) –
kwargs – kwargs to traja.grid_coordinates()

io functions¶

The following methods are available via traja.parsers:

parsers.read_file(id: Optional[str] = None, xcol: Optional[str] = None, ycol: Optional[str] = None, parse_dates: Union[str, bool] = False, xlim: Optional[tuple] = None, ylim: Optional[tuple] = None, spatial_units: str = 'm', fps: Optional[float] = None, **kwargs)¶

Convenience method wrapping pandas read_csv and initializing metadata.

Parameters

filepath (str) – path to csv file with x, y and time (optional) columns
id (str) – id for trajectory
xcol (str) – name of column containing x coordinates
ycol (str) – name of column containing y coordinates
parse_dates (Union[list,bool]) – The behavior is as follows: - boolean. if True -> try parsing the index. - list of int or names. e.g. If [1, 2, 3] -> try parsing columns 1, 2, 3 each as a separate date column.
xlim (tuple) – x limits (min,max) for plotting
ylim (tuple) – y limits (min,max) for plotting
spatial_units (str) – for plotting (eg, ‘cm’)
fps (float) – for time calculations
**kwargs – Additional arguments for pandas.read_csv().

Returns

Trajectory

Return type

traj_df (TrajaDataFrame)

parsers.from_df(xcol=None, ycol=None, time_col=None, **kwargs)¶

Returns a traja.frame.TrajaDataFrame from a pandas DataFrame.

Parameters

df (pandas.DataFrame) – Trajectory as pandas DataFrame
xcol (str) –
ycol (str) –
timecol (str) –

Returns

Trajectory

Return type

traj_df (TrajaDataFrame)

>>> df = pd.DataFrame({'x':[0,1,2],'y':[1,2,3]})
>>> traja.from_df(df)
   x  y
0  0  1
1  1  2
2  2  3

TrajaDataFrame¶

A TrajaDataFrame is a tabular data structure that contains x, y, and time columns.

All pandas DataFrame methods are also available, although they may not operate in a meaningful way on the x, y, and time columns.

Inheritance diagram:

TrajaCollection¶

A TrajaCollection holds multiple trajectories for analyzing and comparing trajectories. It has limited accessibility to lower-level methods.

class traja.frame.TrajaCollection(trjs: Union[TrajaDataFrame, DataFrame, dict], id_col: Optional[str] = None, **kwargs)[source]¶: Collection of trajectories.

TrajaCollection.apply_all(method, **kwargs)[source]¶

Applies method to all trajectories

Parameters

method –

Returns

dataframe or series

>>> trjs = {ind: traja.generate(seed=ind) for ind in range(3)} 
>>> coll = traja.TrajaCollection(trjs) 
>>> angles = coll.apply_all(traja.calc_angle) 

TrajaCollection.plot(colors=None, **kwargs)[source]¶

Plot collection of trajectories with colors assigned to each id.

>>> trjs = {ind: traja.generate(seed=ind) for ind in range(3)} 
>>> coll = traja.TrajaCollection(trjs) 
>>> coll.plot() 

API Pages¶

`TrajaDataFrame`(args, *kwargs)	A TrajaDataFrame object is a subclass of pandas `<~pandas.dataframe.DataFrame>`.
`TrajaCollection`(trjs[, id_col])	Collection of trajectories.
`read_file`(filepath[, id, xcol, ycol, ...])	Convenience method wrapping pandas read_csv and initializing metadata.