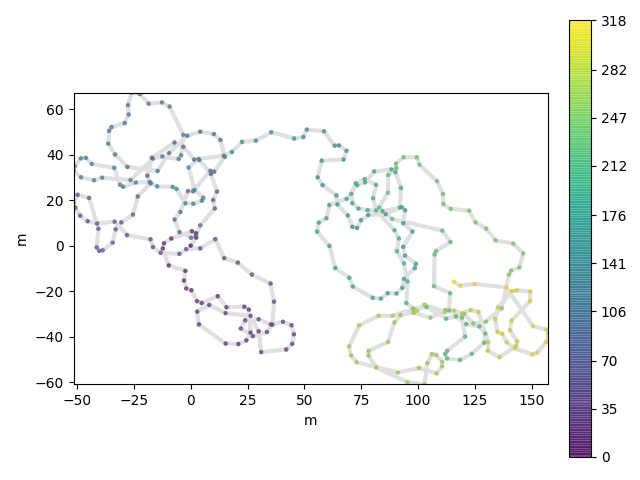
Resampling Trajectories¶
Rediscretize¶
Rediscretize the trajectory into consistent step lengths with rediscretize() where the R parameter is
the new step length.
Note
Based on the appendix in Bovet and Benhamou, (1988) and Jim McLean’s trajr implementation.
Resample time¶
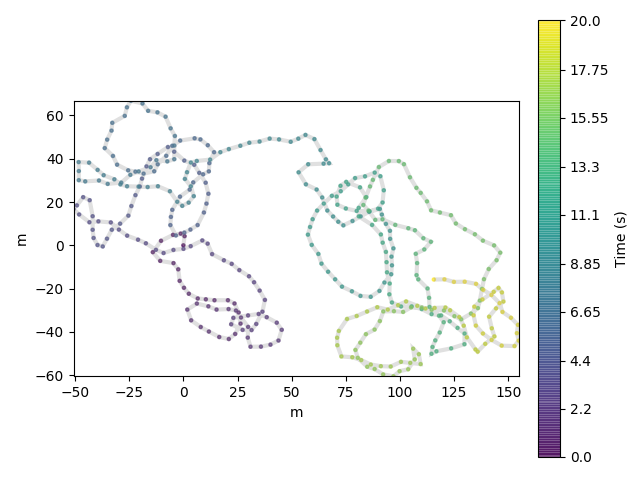
resample_time() allows resampling trajectories by a step_time.
- traja.trajectory.resample_time(trj: TrajaDataFrame, step_time: str, new_fps: Optional[bool] = None)[source]¶
Returns a
TrajaDataFrameresampled to consistent step_time intervals.step_timeshould be expressed as a number-time unit combination, eg “2S” for 2 seconds and “2100L” for 2100 milliseconds.- Parameters
- Results:
trj (
TrajaDataFrame): Trajectory
>>> from traja import generate, resample_time >>> df = generate() >>> resampled = resample_time(df, '50L') # 50 milliseconds >>> resampled.head() x y time 1970-01-01 00:00:00.000 0.000000 0.000000 1970-01-01 00:00:00.050 0.919113 4.022971 1970-01-01 00:00:00.100 -1.298510 5.423373 1970-01-01 00:00:00.150 -6.057524 4.708803 1970-01-01 00:00:00.200 -10.347759 2.108385
For example:
In [1]: import traja
# Generate a random walk
In [2]: df = traja.generate(n=1000) # Time is in 0.02-second intervals
In [3]: df.head()
Out[3]:
x y time
0 0.000000 0.000000 0.00
1 1.225654 1.488762 0.02
2 2.216797 3.352835 0.04
3 2.215322 5.531329 0.06
4 0.490209 6.363956 0.08
In [4]: resampled = traja.resample_time(df, "50L") # 50 milliseconds
In [5]: resampled.head()
Out[5]:
x y
time
1970-01-01 00:00:00.000 0.000000 0.000000
1970-01-01 00:00:00.050 0.919113 4.022971
1970-01-01 00:00:00.100 -1.298510 5.423373
1970-01-01 00:00:00.150 -6.057524 4.708803
1970-01-01 00:00:00.200 -10.347759 2.108385
In [6]: fig = resampled.traja.plot()
Ramer–Douglas–Peucker algorithm¶
Note
Graciously yanked from Fabian Hirschmann’s PyPI package rdp.
rdp() reduces the number of points in a line using the Ramer–Douglas–Peucker algorithm:
from traja.contrib import rdp
# Create dataframe of 1000 x, y coordinates
df = traja.generate(n=1000)
# Extract xy coordinates
xy = df.traja.xy
# Reduce points with epsilon between 0 and 1:
xy_ = rdp(xy, epsilon=0.8)
len(xy_)
Output:
317
Plotting, we can now see the many fewer points are needed to cover a similar area.:
df = traja.from_xy(xy_)
df.traja.plot()